The dark side of “Big Data” A.I.
“How many Youtube cats must Hal see, before Hal calls this a cat?” Bob Dylan, feat. Stanley Kubrick
In the golden age of Artificial Intelligence (a.k.a. AI), it is easy to get fooled by Silicon Valley’s propaganda and the glossy covers of Wired and Time. Since computers can now mimic sophisticated human behavior, such as master Go and – way more human – watch cats on YouTube, we almost have everything solved. Or do we?
What Silicon Valley does not want you to know is that the way in which machines “learn” is not exactly the way you “learn”. Training an AI to play Go cost a whopping 25 million dollars, and machines needed to watch 10 million kittens before being able to reliably recognize one (although, I’ll admit, watching millions of kittens is way cuter than playing 5 million games of Go). An analogy that machines can solve only after reading thousands of War and Peace-sized books, another physical system on this planet can solve just as well – in three seconds:

We usually call them “children”, you know, the mini humans. The gap between human and machine learning is reflected by the difference in time and effort it takes to show a child what a cat is versus a machine. For a child to say, “that’s a cat” you simply have to point to what is a cat and what is not, whereas a machine has to read the entire Wikipedia article on the animal before coming to the same conclusion. This analytical rigor makes off-the-shelf AI very effective in all sorts of data-intensive applications, but very ineffective in a lot of other scenarios (especially in language, as we explained in a previous life).
It is also crucial to note that while the need for data is a scientific challenge, it is also a business one. The race to collect data has led to mounting legal pressure on data collection and data processing, which is challenging many practices around “Big Data” (please note my lawyers say “we are fine”). Additionally, the vast majority of enterprise business cases are not “Big Data”-based, so there will never be the millions of examples that AI requires to learn.
As we shall argue below, AI needs more (and better) ideas, not just more data. The good news is that we can use “Diaper Intelligence” to improve “Artificial Intelligence”, starting with a use case we know very well at Coveo, commerce search.
We believe so much in this idea that we went all the way across the world (Lake Como, what a drag!) to record a TedX talk for Muggles those of you who prefer video stories. And for Muggles those of you that don’t speak Italian – English subtitles are available.
For everybody else, tag along: if you are not scared by math, a very short version of this story (boy, HCOMP 2019 was fun) can be found here.
Interlude: rare words and the “zero result” nightmare
“A problem well-put is half-solved.” John Dewey
Before diving deep into the minds of toddlers, we need to spend one more minute in the realm of adulthood to vividly understand why search engines need to be very good at learning new words. Consider the following eCommerce scenario: a shopper is looking for a “ruffle”, which is a word not included in the product catalog and, therefore, is unlikely to generate relevant results. Uh oh…
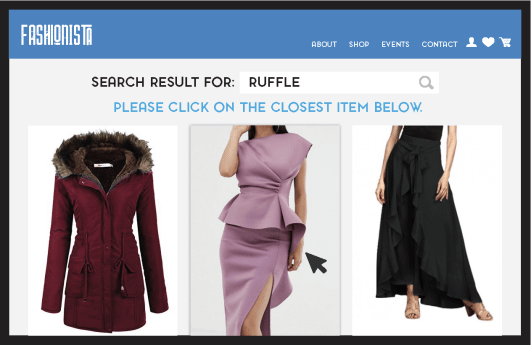
What is the best thing the search engine can do at this point? Well, first, it should know it can’t really solve that query. Second, it should avoid a “zero result” page by trying to engage the user – for example, by asking her a simple question (“Can you please click on the closest item below?”) and nudging her into giving some feedback.
The challenge is therefore the following (remember the ten million kittens above!): how many of these sub-optimal interactions need to happen before the search engine automatically learns that “ruffle” and “peplum” are actually synonyms?
Standard machine learning models won’t really help here. Whereas commonly used search terms can be learned rapidly, the high volume of uncommon or infrequent queries will rarely come up enough to be learned. Thank God we have children to teach us something.
“Learning to learn” from babies
“Tell me and I forget.
Teach me and I remember.
Involve me and I learn.”
Benjamin Franklin
Consider the experimental setting below from a 1986 study conducted by Renee Baillargeon: a six-month-old baby is put in front of a tilted slide, with a toy cart running downhill. The cart slides down, the yellow screen is raised and a colorful cube is shown behind the track – nothing particularly surprising so far.

A 1986 study conducted by Renee Baillargeon. Video attribution: Object Concept VOE Ramp Study Baillargeon.

We now repeat the experiment, with a twist. We raise the yellow screen and show the colorful cube in the middle of the track. When the screen goes down, we trick the kid by secretly moving the cube behind the track and let the cart slide down. As far as the kid knows, the cart passed through the cube this time!

A 1986 study conducted by Renee Baillargeon. Video attribution: Object Concept VOE Ramp Study Baillargeon.

Why is this experiment interesting or relevant for doing machine learning in a search engine? (Bear with us, the devil is in the detail!)
The six-month-old baby does not know physics, so he certainly cannot tell us that “a solid body can’t go through another solid body”. What does the baby know about the cart and the cube, though?
The picture below shows the baby’s reaction for each of the two scenarios and leaves little room to doubt that the impossible reality was not what he expected.

A baby observing possible vs. impossible physical scenarios: he may not know how to explain his physical intuition with his words, but his face says a lot!
This is lesson number one: babies have a lot of “theories” about how the world works and all sorts of expectations for how things will behave, even if they can’t tell us. In other words, to learn quickly, it is very useful to already know something.
Theories – for kids as well as adults – are useful because they guide exploration. They are mental models that can be used to simulate reality and make specific predictions. It shouldn’t really surprise us that evolution equipped babies not just with theories, but with some scientific method as well. When given the choice between the “regular” toy car and a “physics-defying” toy car, the baby will prefer to play with the latter. Moreover, a scene from a 2015 study by Johns Hopkins University researchers Aimee E. Stahl and Lisa Feigenson shows what happens when the baby first “plays” with the strange toy that seemed to pass through the box:

A 2015 study by Johns Hopkins researchers Aimee E. Stahl and Lisa Feigenson reveals that a baby choosing to “play” with a surprising new toy will first “test” the toy. Video by: Len Turner, Deirdre Hammer and Dave Schmelick, Johns Hopkins University Office of Communications.
The baby is testing the solidity of the object, since his “theory” of solidity has been challenged by the experiment – it has violated his expectations. This is his way of verifying what he knows to be true. In fact, if we trick him again (bonus lesson: it is very easy to trick infants!) by showing him a toy car going upwards in the sky instead of falling, like gravity predicts, the baby will “play” with the car by dropping it from the high-chair – he is not testing solidity anymore, he is testing “resistance to gravity”.

This is lesson number two: learning is an active process. Our babies are way more similar to little scientists, using the environment to test their predictions, than to sponges, which passively absorb substances floating randomly around them.
If you compare lesson one and lesson two with any neural network tutorial (there are as many AI videos as kittens these days), you should immediately realize why “learning” is still so different for humans and machines. The “learn-from-scratch” method deployed by deep learning systems has allowed for great progress (especially in image-based tasks), but it is still far from being as efficient as human learning.
The good news is that we can build cutting-edge AI that mimics the best abilities of children. Let’s start with search engines.
How search engines learn new words
“Arrest this man / he talks in math.”
Radiohead, Karma Police
Remember our “ruffle” challenge: how can a search engine quickly learn the meaning of new words through only a few shopper interactions? We can now reassess this in the light of what Diaper Intelligence has taught us.
Lesson number one: our AI needs to know something about physics clothes; for example, that dresses come in different types, and that a pair of shoes can be either flats or boots – but not both. Structured information about a domain is called “ontology” / “taxonomy” / “knowledge base”, but recently the fancier “knowledge graph” (a.k.a. KG) seems to be the winner (all the cool kids are doing it!).
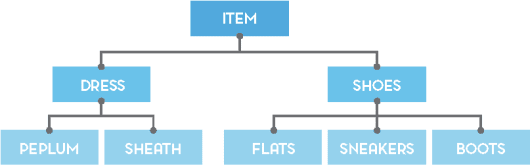
A simple KG for fashion clothes: items are either dresses or pairs of shoes, which in turn are divided into more specific types (e.g. flats vs. boots).
KGs play a crucial role in learning by providing symbolic theories that constrain the space of plausible hypotheses to consider:
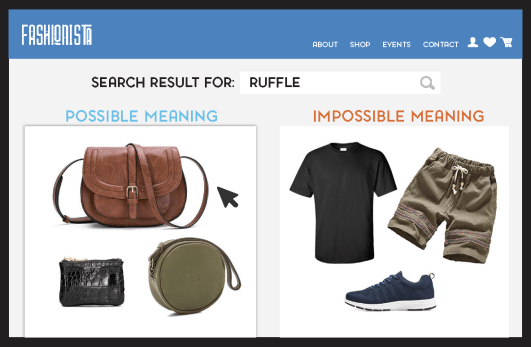
The structure of the KG allows the system to concentrate on “possible” meanings, without considering unlikely bundles of objects.
While humans have a word for the set of objects on the left (i.e. “bags”), humans won’t likely have a word for the set of objects on right (in fact, there is no such word as “sneakers-shirt-skirt”). In numerical terms, a KG just cut down the number of possible meanings for “ruffle” from 2|P| (where |P| is the number of products on a commerce site) to a handful of nodes. In the words of this fantastic work on lexical learning, “a structured hypothesis space [is] the most important component that supports learning from few examples.”
And now, a question to introduce lesson number two: how can a search engine conduct experiments since it only “lives” in your browser? The answer is obviously you. By using your feedback (in the form of clicks over products after you searched for “ruffle”), the AI tests the meaning hypotheses generated with its knowledge graph. In the mind of the machine, shoppers are the metaphorical equivalent of a table on which to smash toys.
If we put lesson one and lesson two together, our AI can determine the correct meaning of “ruffle” after only a couple of clicks, as we will show below. Consider the following KG and the unknown word “ruffle”:
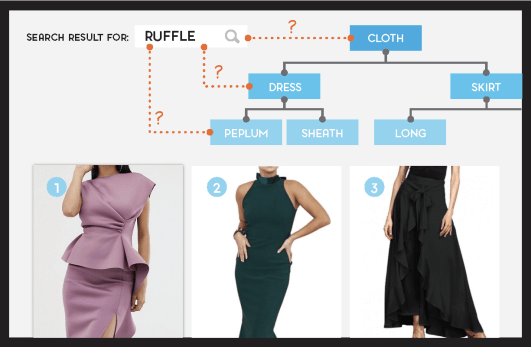
A simple KG: what is the meaning of ruffle?
We can test (a simplified version of) the learning algorithm with this WebPPL script : press RUN and see what the system thinks about the possible meanings for “ruffle” given the feedback it received on product 1. (If you’re done with Netflix, a “conceptual” introduction to probabilistic programming in A.I. can be found here.)
///fold: represent ontology
// specify the extension of the concepts
var extensions = {
'peplum': ['1'],
'sheath': ['2'],
'dress': ['1', '2'],
'skirt': ['3', '4'],
'long': ['3'],
'mini': ['4'],
'cloth': ['1', '2', '3', '4']
};
// put some priors on the space of categories in the ontology tree
var ontologicalTree = Categorical({
'ps': [0.2, 0.5, 0.3, 0.3, 0.5, 0.3, 0.3],
'vs': ['cloth', 'dress', 'peplum', 'sheath', 'skirt', 'long', 'mini']
});
var learningModel = function() {
var hypothesis = sample(ontologicalTree);
var ext = extensions[hypothesis];
var obsFn = function(datum){condition(
any(function(x) { return x == datum; }, ext)
? flip(Math.pow((1.0/ext.length), shopperSuggestions.length)) : false)}
mapData({data: shopperSuggestions}, obsFn)
return hypothesis;
};
///
var shopperSuggestions = ['1'];
///fold: perform probabilistic inference
var m = Infer({
method: 'MCMC',
samples: 1000,
model: learningModel
});
///
viz(m);
Now, change the shopperSuggestions line to:
var shopperSuggestions = ['1', '1'];
and see how the distribution changes: undecided at the first interaction (“peplum” vs. “dress”), and then very confident after the second! If you feel very adventurous, go through our wip paper to understand the details of the Bayesian approach we chose.
Growing a(n artificial) mind: what’s next?
“We are stuck with technology
when what we really want is just stuff that works.”
Doug Adams
Building a commerce search engine is no small feat, and lexical inference is only one of the many challenges that AI needs to solve. We are definitely not the only ones arguing for a business and scientific assessment of current machine learning practices (people we like a lot are too) and for the “injection” of cognitive ideas into the mix. If we want to build an “intelligent” system, it seems only natural that we start by looking at what really intelligent systems, such as children, do every day.
As we are actively working to bring KG-based inferences into a scalable product, it is mildly amusing to note at the end of this post that you have also been tricked. In particular, recall the products that our search engine shows to shoppers when the meaning of “ruffle” is still unknown:

Why did AI pick those three specifically? Isn’t it a bit too convenient that among thousands of products we selected a peplum dress that users can click on? The truth is, we cannot know exactly which products to show, but we can design a system that intelligently picks (like children do) which products are the best to test.
The details of “optimal experiment design” are awesome, but unfortunately this blog is too narrow to contain them (you will find the Appendix below more spacious, though).
Final lesson: scientists will distract you to let you think they have it all figured out.
See you, space cowboy
If you liked our short paper and want to know how we are extending the approach from a small knowledge graph to a business case with 30k products, please get in touch with us.
If you also believe – like us and HBR – that the future is about less data, not more, don’t forget to follow us on LinkedIn to stay up to date with AI Labs initiatives.
Acknowledgements
Thanks to Andrea Polonioli and Ciro Greco for feedback on previous versions of this work. Special thanks to Reuben Cohn-Gordon, who co-authored our HCOMP paper and was instrumental in clarifying many of the technical details behind the scenes.
Appendix: how do we pick our products intelligently?
As explained above, the thoughtful testing of competing hypotheses is a crucial component of children’s ability to learn quickly, and it is something we would like our machines to be able to mimic. Unsurprisingly, people in the actual business of testing hypotheses all day – i.e. scientists – have devoted quite some time and energy to answer the following question: given a space of possible experiments I can run (and assuming I can’t run them all), how do I select the ones that will be most effective in distinguishing between hypothesis X and Y?
The mathematical details of this answer have been known for a while, but most systems performing optimal experiment design (OED) are too specialized to enjoy widespread use (note: recently some nice and clever people built a WebPPL plugin!).
Before addressing the problem of picking products on a commerce site, let’s start with a simpler example. I will give you four coin tosses and ask you to predict the next value in the sequence. I have two competing hypotheses in my mind about your prediction process:
- H1: you think that the coin is fair (i.e. probability of head = probability of tail = 0.5)
- H2: you think that the coin is biased (i.e. probability of head != probability of tail)
The space of possible experiments I can run to distinguish between H1 and H2 is obviously all the possible sequences of H and T in a four-item sequence. Let’s analyze two extreme cases, shown in the figure below, to make our point.
- E1: I give you HHTT and ask you to predict the fifth value
- E2: I give you HHHH and ask you to predict the fifth value

My goal as a scientist is to pick the “optimal” experiment between E1 and E2 to distinguish between H1 and H2. To do that, I need to consider (figure above, on the right) the predictions you would make assuming H1 vs. H2. It is clear, in fact, that after a sequence such as HHTT your prediction for the fifth value will be exactly the same for both hypotheses:
- If you think the coin is fair, you will predict head with 50% probability;
- If you think the coin is biased, no bias can be learned from a HHTT sequence, so you will still predict head with 50% probability.
Following the same reasoning, we find that your prediction after HHHH will differ assuming H1 vs. H2:
- If you think the coin is fair, you will predict head with 50% probability (as usual);
- If you think the coin is biased, from HHHH you will conclude a head-bias, and therefore you will predict head with >50% probability.
In other words, HHHH is a more informative experiment, since it allows the scientist (me) to distinguish between competing hypotheses given the feedback from the subject (you). Use of the term “informative” is intentional. We can make the reasoning above general and rigorous using the concept of expected information gain (EIG), such that picking the ideal experiment to run is equivalent to picking the experiment with the highest EIG.
Going back to our product scenario, consider this toy KG, with 5 nodes and products: P1, P2, P3, P4, belonging to different types ( P1 is a peplum dress for example, P4 is a pair of shoes, etc.).
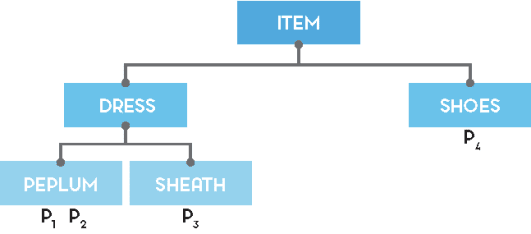
Given all possible product bundles of size n, we need to show the bundle b* that maximizes EIG, given all possible User choices, that is:
b* = argmax(b) Ep(y; b) DKL(P(h) | b, y) || P(h))
(where Ep(y; b) is the probability of observing click y for bundle b and DKL is the KL-divergence)
Practically, if you do the calculations for the KG in the picture and n=2, this is the ranking of bundles by EIG:
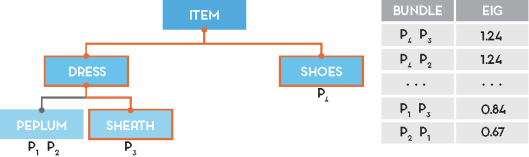
Not surprisingly, the EIG formal criteria matches our intuition: <P1, P2> is a fairly not an interesting experiment to run for the machine, as any click won’t falsify any hypothesis (<P1, P2> is the equivalent of the non-informative experiment HHHH in our coin example); on the other hand, <P4, P3> is a highly informative bundle, as the selected products cover a wide portion of the KG: a User click on P4 will be, for example, very telling about which hypothesis is likely to be true.


